発達障害の子にものを数えることを教えるには

2019.09.12
※この記事は約10分で読めます。

こんにちは。
四谷学院療育講座、55レッスンのブログ担当 neco です。
今回の記事では、「数えること」について少し深掘りして考えてみましょう。


監修：計野 ちあき（言語聴覚士）
ことばの発達相談室ほっとほっと代表
都内の市や区において指導や研修を担当。言葉と発達相談室 ほっとほっとでは、言葉の発達やコミュニケーションに関しての相談を伺い、お子様の発達に合わせた指導を行っている。詳しいプロフィールはこちら。

数えるということ

わたしたち大人は普段、何気なく数を数えています。
あまりにも自然に行っていることなので、自分がどうやって数えているのか、どうやって数え方を覚えたのか、意識している方はほとんどおられないでしょう。

それほど自然な行為である「数えること」ですが、人が数を数えることの裏には、実は非常に複雑なステップが積み重なっています。
発達に偏りがあったり、理解に得意不得意があったりすると、数を数えることに難しさを感じることも。
数を数える行為を分析していくことで、そんな時の支援のヒントが見えてきます。

数字と数詞と個数

「数がわかる」とは、「数字」「数詞」「個数」という3つの概念を結びつけることです。

数字＝１、２、３・・・のような、数の表記
数詞＝いち、に、さん・・・のような、数の言葉
個数＝○、○○、○○○・・・のような、実際のモノの数量

この3つの概念を自由自在に行き来できるようになることが、「数えられるようになること」だと言えるでしょう。

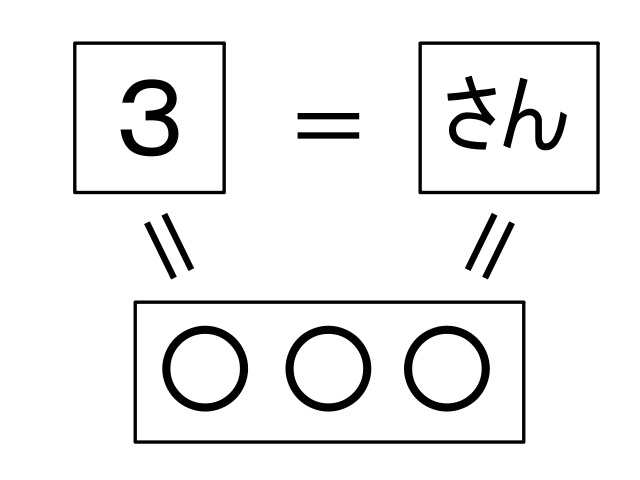
▲この図にある「○○○」のような、個数を表現する図を「数図」と呼びます。

数唱と計数の違い

数えることには、大きく分けて2つの側面があります。
一つが「数唱（すうしょう）」、もう一つが「計数（けいすう）」です。
この二つは、まったく別の概念です。

▲数唱と計数の違いを知ると、数の指導がわかりやすくなります

数唱

ご家庭で「数をおしえる」というと、まず真っ先にイメージするのが「イチ、ニ、サン、シ･･･」と、数の言葉を伝えることではないでしょうか。
これが「数唱」です。
数唱ができるとは、数を表す言葉と、その順番が正しくわかることです。

▲お風呂で「10まで数えようね」「イーチ、ニーイ･･･キューウ、ジュウ！」などのやりとりも、立派な数唱の練習です

計数

一方、計数とは、モノの数量を数えること、ものの個数を把握することです。
目の前にリンゴが3個並んでいたとして、それを「3個」と数え、3という数量を把握することが「計数」です。

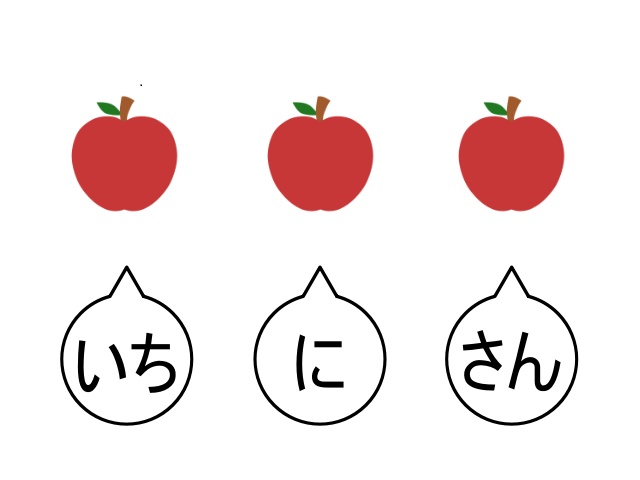
▲リンゴが3個あるとわかることが、計数ができるということ

数唱と計数の理解の深まり

数唱ができなければ正確な計数はできません。
が、数唱ができただけでは、正確な計数ができるようになるわけではありません。
数唱と計数のどちらにも、さまざまな理解の段階があります。

▲数唱と計数のそれぞれの理解の段階がわかると、指導の次の一手を工夫しやすくなります

数唱の理解

まずは数唱から見ていきましょう。
数唱ができるようになったと言えるためには、どのような要素が考えられるでしょうか。

数の表現

日本語で数を表すには、さまざまな表現があります。

■イチ、ニ、サン、シ･･･
■ヒトツ、フタツ、ミッツ、ヨッツ･･･
■イッコ、ニコ、サンコ、ヨンコ･･･
■ヒトリ、フタリ、サンニン、ヨニン･･･

「シ」は「ヨン」とも言いますし、「ナナ」は「シチ」とも言います。
一つの数字に二通りの呼び方があることを納得し、場合によって使い分ける必要が出てきます。

さらに、日本語では、数える対象によっても表現が変わります。
人なら「人」、本なら「冊」、車なら「台」、動物なら「匹」といったように、それぞれ異なる単語（助数詞）をくっつける必要があります。
「フタリ」と「ニサツ」、まったく表現が違うのに、表しているのはどちらも同じ「2つ分のモノ」のことですね。
この複雑な表現を丁寧に覚えていく必要があります。

助数詞を使いこなすのは単純な数唱よりも少し先の学習になりますが、これらの数の表現を正確に覚え、何を表しているかを知ることが大切です。

数の系列の分割

よく、小さなお子さんが、こんなふうに数を唱えているのを耳にします。

「イチニイサンシイゴオロクシチハチキュウジュウ！」

これを聞くと、大人は、この子は1から10までの数を言えるようになったのだと考えます。
ところが中には、この呪文のような長い文句を全てひとつながりの言葉だと捉えていて、独立した10個の数字のことを意味していると理解していない場合があります。
確認するためには、ちょっとひねった質問をしてみましょう。

■10から1まで降順で唱える（ジュウ、キュウ、ハチ、ナナ･･･）
■8の次の数を言う

このような質問に適切に答えられない場合は、数の系列をしっかりと理解している、数の言葉（数詞）それぞれを独立した言葉として理解している、とは言い切れません。
一つずつの数について、より丁寧に理解をはぐくむ必要があるでしょう。

数字と数詞の結びつき

数を使いこなすためには、1＝イチ、2＝ニ、3＝サン、といったように、数の表記の仕方（数字）と数字の呼び名（数詞）を結びつける必要があります。

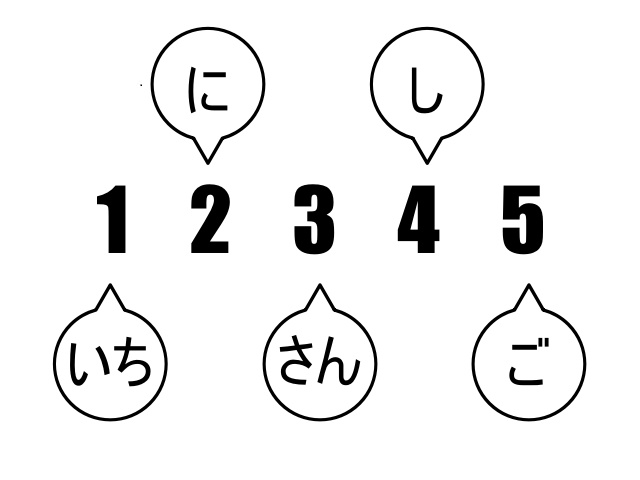
▲数字と数詞を結びつける

よくある数の学習教材として、1から10までの数字を順番に並べ、数詞（イチ、ニ、サン･･･）と数図（●、●●、●●●･･･）を書き加えたものなどが市販されています。
大人の目からはなんということもない教材のようですが、＜数字、数詞、個数、数の順番＞と、いくつもの概念を同時に伝えようとしているわけで、実はなかなかに高度な内容を扱っています。

このような教材を使って学習してもなかなか数の理解が進まない場合、その子は数の理解がもともと苦手だったり、複数の概念を同時に把握するのが難しかったりするのかもしれません。
数を一つずつ提示して数字と数詞を教える、言われた数字を選ぶ、一つひとつの概念を切り離して教える働きかけを模索してみるとよいでしょう。

計数の理解

次に、計数です。
計数ができるようになったと言えるためには、どのような要素が考えられるでしょうか。
計数の五原理という考え方に基づいて見ていきましょう。

一対一対応

モノを数える時には、一つのモノに一つの数の言葉を当てはめます。
これを「一対一対応」と呼びます。
一つのモノに対して二つの数の言葉を当てはめたら、正確に個数を把握することはできませんね。

モノを一つずつ指さしながら「イチ、ニ、サン･･･」と数えていくような作業も一対一対応です。
よく見られるのは、1個・2個・3個くらいまでは指の動きとカウントが合うのだけれども、数が大きくなっていくにつれて、最後の方では指とカウントがバラバラになってしまう、といった場合です。
この場合は、一対一対応の練習をもう少し深めるとよいと考えられます。

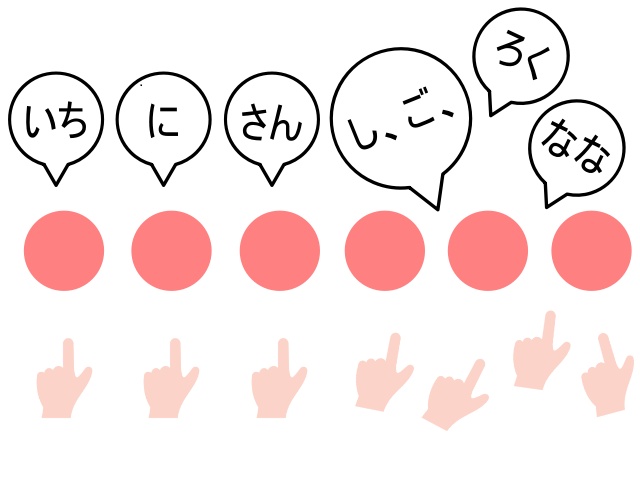
▲数が大きくなるほど指の動きとカウントが合わなくなることがある

安定順序

モノに数の言葉を当てはめる時には、必ず一定の順序で当てはめる必要があります。
「イチ、ニ、サン、シ、ゴ」と正しい順序で当てはめられるからこそ「5個」が割り出せるのであって、「イチ、ニ、サン、ゴ、ナナ」と、数の言葉を間違った順序で当てはめてしまってはいけないのです。
モノに対して数の言葉を決まった順番通りに当てはめられること、これを「安定順序」と呼びます。

数唱を覚えたてのお子さんには、安定した順序を保てないことも間々見られます。
数唱をしっかり練習したり、数列を視覚化したりすることで、数字の順番の理解を深めるとよいと考えられます。

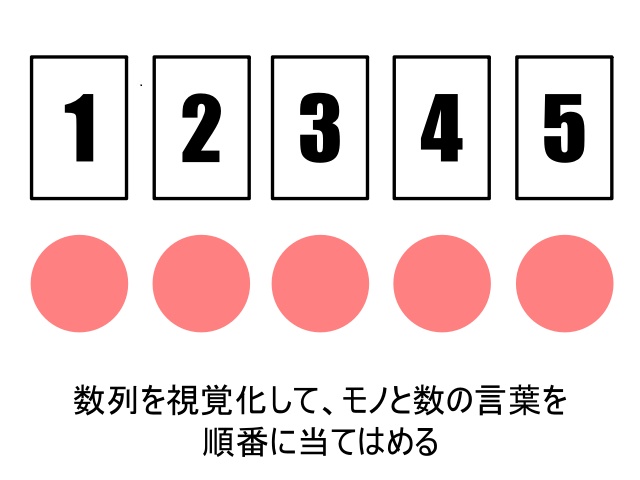
▲数の順番を明確にし、安定した順序を保ちやすくする例

基数性

モノに数の言葉を一つずつ当てはめていって、最後に当てはめた言葉が、そのモノの集合の数量を表します。
これを「基数性」と呼びます。
最後の言葉の役割を理解できていない場合は、いくつある？と問われても、「イチ、ニ、サン、シ、ゴ」と唱えるだけで、「5個」という答え方を導き出せないことがあります。

基数性は、計数の五原理の中でも教え方が難しいと感じる方が多いように思います。
「ゴコ」という答えを復唱させたり、数の言葉と個数との関係を文字や数字で視覚化したり、といった支援が考えられますが、その子にとってわかりやすい見せ方をよく考えながら働きかけを工夫したいところです。

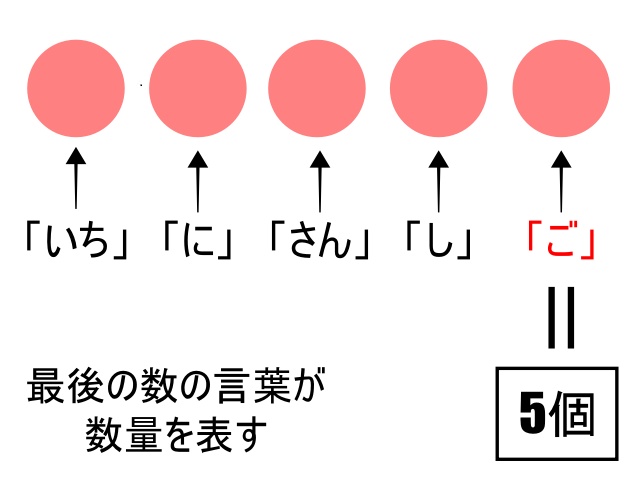
▲「イチ、ニ、サン、シ、ゴ」と「5個」の間にある概念の壁は意外と大きい

順序無関係

モノを左から数えようと、右から数えようと、真ん中から数えようと、全体の個数に変化はありません。
どこから数えたとしても量は一緒で、数える順番と個数に関連性はない、とするのが「順序無関係」の考え方です。

necoの個人的な感覚ですが、順序無関係の考え方に戸惑うお子さんはそれほど多くない印象があります。
モノを整列させて端から数えることを教わるお子さんが多いため、順序無関係を意識する機会も少ないのかもしれません。
きれいに並べられたモノを端から数える中で、バラバラに（順序無関係に）数えると数えにくい、数え間違う可能性がある、ということも伝えていけると良いですね。

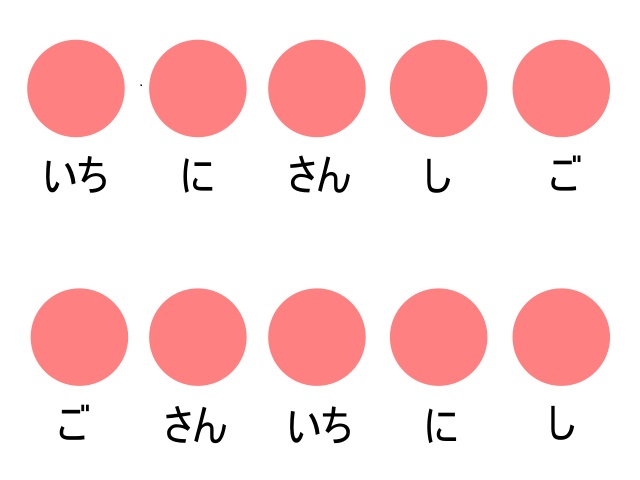
▲どこから数えても5個は5個

抽象性

どんな色、形、大きさのモノでも、1個は1個です。
リンゴでも1つ、鉛筆でも1つ、自動車でも1つ、、、といったように、モノそのものの属性を抜きにして、数量という概念だけを取り出せることが「抽象性」という考え方です。

たとえばリンゴとスイカを並べて数えた時に、リンゴを順調に数え進んでいって、スイカまで来た時にカウントが止まったら、その子はスイカの属性に引っかかっている可能性がありそうです。
見た目の違いに戸惑ってカウントから意識が逸れてしまったり、小さなリンゴは1個で良さそうだけれども大きなスイカまでも1個と数えてよいのか迷ったり、しているのかもしれません。
このような時は、まずは見た目もサイズもさまざまなモノを並べて数える体験を繰り返すことが練習の第一歩となるでしょう。

▲「リンゴ3個とスイカ1個で全部で4個」がわかるのは、計数の抽象性が育っているから

 

数えることについてまとめ

いかがでしたか。
数えるという行為にいかに多くの要素が含まれているか、おわかりいただけたかと思います。
これだけ複雑な数の学習を深めていくためには、学びの足掛かりもたくさん用意してあげる必要があります。

55レッスンでも、「数えることができない」というご相談をしばしばいただきます。
が、一言で「数えられない」といっても、その子が今どこでつまずいているかによって、効果的な支援は全く変わってきます。
数唱ができないのか、一対一対応が不十分なのか、それ以前の学習に対する向き合い方の問題なのか･･･
55レッスンの担任は、学習の状況を色々と確認しながら、その子の学びを深める働きかけを工夫していきます。

目の前のこの子が、今、どこまで、何を、理解できているか。
それがわかれば、支援の工夫はきっと見つかります。
この記事が、数の学びの道のりを想像するためのお手伝いになれば幸いです。

こちらは、自閉症・発達障害の療育 四谷学院55レッスンのブログです。
55レッスンは、自閉症・発達障害のお子さんがご家庭で親御さんとご一緒に学べる療育の通信講座です。

我が子にとってより良い働きかけを工夫したい、もっと気軽に誰かに相談したい･･･
そんな思いをお持ちの保護者様は、ぜひ一度、HPをご覧ください。


＼＼クリック／／

コメント